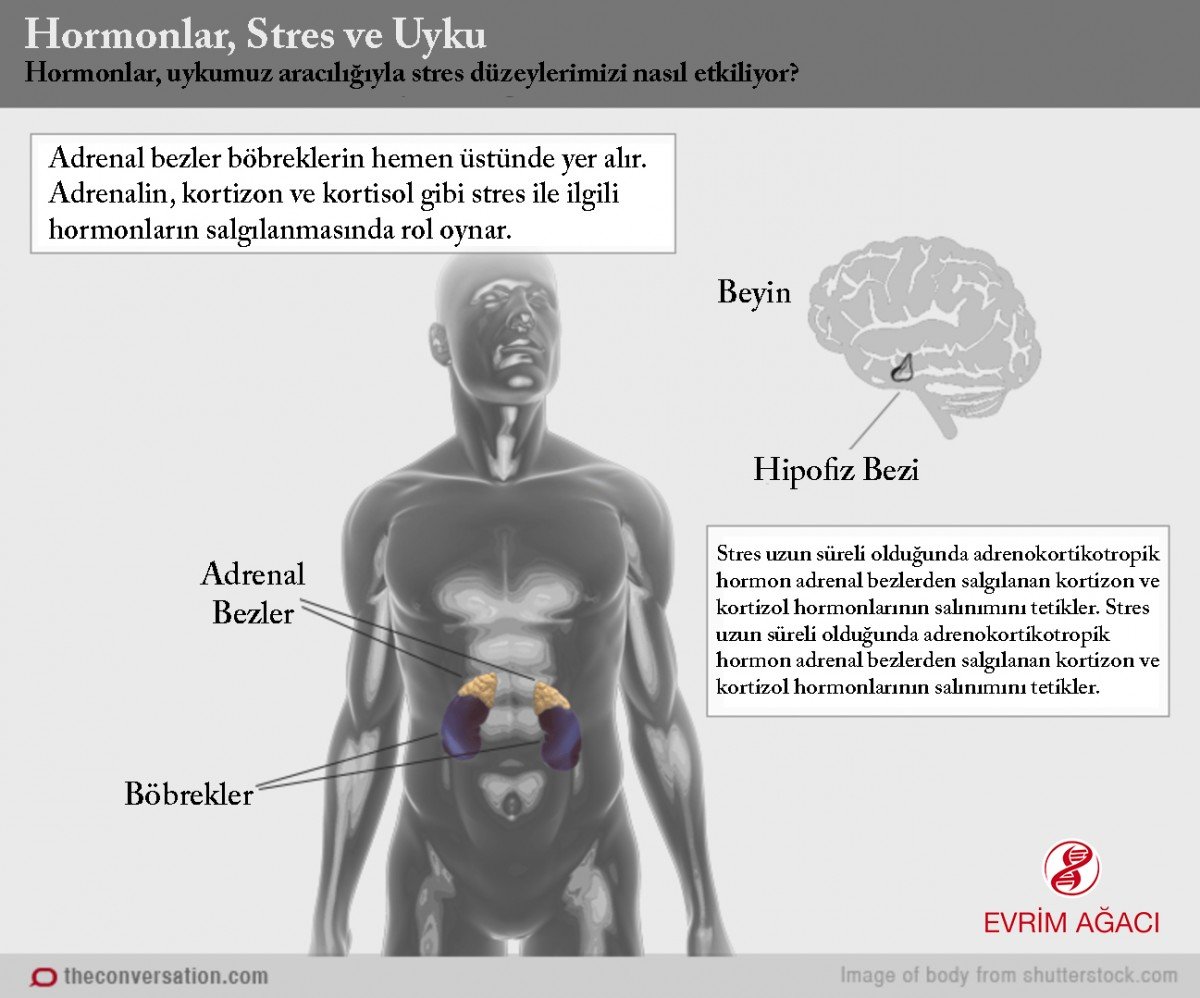
Sinonim: vena cava inferior, inferior vena cava (IVC), Untere Hohlvene.
Alt ana toplardamar. (bkz: vena) (bkz: kava) (bkz: inferiyor)

Tıp terimleri sözlüğü
Tanım ve Terminoloji
“Sol akciğer alt toplardamarı” ifadesi, anatomik olarak vena pulmonalis sinistra inferior teriminin Türkçeleştirilmiş şeklidir. Bu damar, sol akciğerin alt lobunda oksijenlenmiş kanı kalbin sol atriyumuna (atrium sinistrum) taşıyan, dolayısıyla pulmoner dolaşımın venöz bileşenine ait olan bir yapıdır. Bu terim şu parçalardan oluşur:
Bu bağlamda vena pulmonalis sinistra inferior, sol akciğerin alt lobundan çıkan ve kalbin sol kulakçığına yönelen oksijenli kanı taşıyan bir damardır.
Anatomik Konum ve Yapısal Özellikler
İnsan vücudunda toplam dört adet pulmoner ven bulunur: sağ üst, sağ alt, sol üst ve sol alt pulmoner ven. Bu dört damar, her iki akciğerin loblarından oksijenlenmiş kanı sol atriyuma getirir. Bunlar:
Sol akciğer, iki loba sahiptir: lobus superior (üst lob) ve lobus inferior (alt lob). Sol alt lobdan gelen kan, segmental venöz dallar yoluyla birleşerek vena pulmonalis sinistra inferior adlı ana toplardamarı oluşturur. Bu damar daha sonra hilum pulmonis’ten çıkarak mediastenum üzerinden kalbin sol atriyumuna ulaşır.
Sol alt pulmoner ven, hilum pulmonisten geçerken bronşiyal yapıların alt kısmında ve pulmoner arterin posteriorunda (arkasında) yer alır. Pulmoner venlerin hilum içindeki yerleşimi şu şekilde tanımlanır:
Bu tipik yerleşim düzeni, “VAB” (vena–arteria–bronchus) akronimiyle akılda tutulabilir.
Fizyolojik Rol ve Kan Akışı
Vena pulmonalis sinistra inferior, sol akciğerin alt lobundan toplanan oksijenlenmiş kanı sol atriyuma iletir. Akciğerlerde gerçekleşen gaz değişimi sonrasında, alveollerden çıkan oksijen açısından zengin kan pulmoner venüller aracılığıyla segmental venlere, oradan da lobar venlere ve nihayetinde ana pulmoner venlere katılır.
Bu oksijenli kan, sol atriyuma ulaştıktan sonra mitral kapak aracılığıyla sol ventriküle geçer. Buradan da aort yoluyla tüm vücuda pompalanır. Dolayısıyla vena pulmonalis sinistra inferior, sol sistemik dolaşımın başlangıcındaki en kritik yapılardan biridir.
Histolojik Özellikler
Pulmoner venler histolojik olarak diğer sistemik venlerden bazı farklılıklar gösterir:
Bu histolojik yapı, düşük basınçlı fakat yüksek oksijen içeriğine sahip kanın düzgün taşınmasını kolaylaştırır.
Klinik Önemi
Embriyolojik Gelişim
Pulmoner venler, embriyonik gelişimde ilk olarak tek bir pulmoner venöz kök aracılığıyla sol atriyuma bağlanırlar. Zamanla bu kök dallanarak dört ayrı pulmoner vene dönüşür. Bu sürecin anormal seyretmesi, konjenital anomalilere neden olabilir. Sol alt pulmoner venin gelişimi, sol arka kardinal ven sisteminden bağımsız olarak pulmoner sinüslerden türemektedir.
Sol akciğer alt toplardamarı — yani vena pulmonalis sinistra inferior — anatomik literatürde yer alan dört ana pulmoner venden biridir. Bu damar, hem fonksiyonel olarak hem de tarihsel olarak büyük öneme sahip bir yapıdır. Ancak bu damarın ve genel olarak pulmoner venlerin keşif tarihi, insan vücudunun dolaşım sistemi hakkında yüzyıllar süren kavramsal dönüşümlerle iç içedir. Bu süreç; antik dönem yanlış anlamaları, Rönesans dönemi otopsi bulguları, mikroskopik keşifler ve modern anatomi atlaslarının gelişimiyle şekillenmiştir.
İlk sistematik anatomi bilgileri, Hipokrat (M.Ö. 5. yy) ve Galenos (M.S. 2. yy) gibi hekimlerin eserlerinde yer aldı. Ancak bu dönemde pulmoner dolaşımın ayrıntılarından söz edilmez.
Sol akciğer alt lobundan gelen venöz dönüşle ilgili özel bir farkındalık bu dönemde yoktu. Damarlar fonksiyonel kategorilere göre değil, anatomik görünüme göre adlandırılıyordu.
İbn Sina (980–1037) ve İbn Nefis (1213–1288), Galenos’un teorilerine eleştiriler getirerek pulmoner dolaşım hakkında daha gerçekçi görüşler sundular.
Bu dönemde mikroanatomik yöntemlerin gelişmesiyle birlikte akciğer lobları ve ilgili damarların sınıflandırılması yapılmaya başlandı.
Son yıllarda bu damar, sadece anatomik bir yapı değil, aynı zamanda çeşitli klinik uygulamalarda odak noktası haline gelmiştir:
Dolayısıyla “vena pulmonalis sinistra superior” ifadesi, “sol akciğerin üst kısmından gelen ve sol kulakçığa dökülen oksijenli kanı taşıyan toplardamar” anlamına gelir.
Sol akciğer üst toplardamarı, latince ifadesiyle vena pulmonalis sinistra superior, akciğerlerden oksijenlenmiş kanı toplayarak kalbin sol kulakçığına (atrium sinistrum) taşıyan dört ana pulmonal venadan biridir. Bu damar, yalnızca anatomik konumuyla değil, aynı zamanda histolojik yapısı, embriyolojik kökeni ve klinik önemiyle de ayrıntılı incelenmeyi hak eden bir yapıdır.
Sol akciğer üst toplardamarı, sol akciğerin üst lobundan (lobus superior pulmonis sinistri) ve kısmen de lingula adı verilen bölgesinden gelen oksijenlenmiş kanı toplar. Bu damar, hilum pulmonis düzeyinde (akciğerin vasküler ve bronşiyal yapılarının giriş-çıkış yaptığı anatomik bölge) oluşur. Buradan çıkarak mediastene yönelir ve kalbin sol atriyumuna açılır.
Komşuluk açısından değerlendirildiğinde:
Sol akciğer üst toplardamarı, hiluma girmeden önce genellikle 2-3 segmental venöz dalın birleşmesiyle oluşur. Bunlar çoğunlukla:
şeklinde dallanır. Bu segmental venler segmental bronş ve arterlerle birlikte segmentum bronchopulmonale olarak adlandırılan işlevsel ve anatomik alt birimlere hizmet ederler.
Pulmonal venler histolojik olarak ince tunika media‘ya sahiptirler ve bu yönüyle sistemik venöz yapılardan ayrılırlar. Endotel iç yüzeyi, düşük dirençli bir akışa olanak tanıyacak şekilde düzenlenmiştir. Damar çapı geniştir ve kalbe doğru yönelen sürekli bir kan akımı taşır.
Pulmonal venler embriyogenez sırasında sol atriyumun dorsal duvarından tomurcuklanarak gelişirler. Başlangıçta tek bir pulmonal ven söz konusudur. Bu yapı zamanla dört ana ven olacak şekilde dallanır ve sonunda her biri bir akciğer lobuna karşılık gelen damarları oluşturur. Sol akciğerin üst lobuna giden venöz drenaj da bu süreçte gelişir.
Sol akciğer üst toplardamarı, birçok klinik senaryoda önem arz eder:
Sinonim: Vena pulmonalis dextra inferior, right inferior pulmonary vein.
Sağ akciğer alt toplardamarı.(Bkz; Vena) (Bkz; pulmonalis ) (Bkz; dekstra) (Bkz; inferior)
Sinonim: Vena pulmonalis dextra superior, right superior pulmonary vein.
Sağ üst akciğer toplardamarı. (Bkz; Vena) (Bkz; pulmonalis ) (Bkz; dekstra) (Bkz; superior)



 Muayenehanede doktorun karşısında sessizce oturuyorsunuz. Doktor üzgün bir ifadeyle konuşmaya başlıyor:
Muayenehanede doktorun karşısında sessizce oturuyorsunuz. Doktor üzgün bir ifadeyle konuşmaya başlıyor:
“Test sonuçlarınız geldi. Maalesef, pozitif!”
“Hasta mıyım yani, emin misiniz?”
Başını sallıyor: “Testin doğruluğu çok yüksek. O yüzden, maalesef hemen hemen eminim. Tedaviye başlamamız lazım. Bu nadir görülen bir hastalık olduğu için kesin bir tedavi henüz bulunamadı, ama elimizden geleni yapacağız.”
Boğazınız kurumuş, yutkunuyorsunuz. Birkaç saniye ikiniz de sessizce oturuyorsunuz. Sonra aklınıza birşey geliyor.
“Yapılan testle kanımdaki bir maddeyi ölçüyorsunuz değil mi?”
“Evet. Bu hastalık her zaman bu maddenin üretilmesine sebep olur. Madde mevcutsa test muhakkak tespit eder.”
“Peki başka sebeple oluşmaz mı bu madde?”
“Nadiren, yüzde bir ihtimalle genetik sebeplerle de olur, hastalıkla ilgisi olmadan.”
“Ama…” Duraksıyorsunuz. Şoka rağmen kafanızın dişlileri çalışmaya başlıyor. Doktor acıyan gözlerle size bakıyor. Kötü haber alanların ilk yaptığı şey inkar etmektir zaten, biliyor.
“Size şimdi bir sevk…” diye başlarken sözünü kesiyorsunuz.
“Hastalık nadir görünüyor demiştiniz. Ne kadar nadir? Toplumdaki görülme sıklığı ne kadar?”
“Yani şimdi, ne bileyim….”
Doktorun yüzü asılıyor. Sorgulayıcı hastalardan hoşlanmadığını yüzünden okuyorsunuz. Ama sözkonusu olan sizin hayatınız, cevapsız kalmayı kabul etmiyorsunuz. Bekliyorsunuz.
“Onbinde bir filandır herhalde.”
“Tamam!” Doktorun masasından bir kağıt ve kalem kapıp birşeyler karalamaya başlıyorsunuz. Doktor sabırsızlanıyor, ama oralı olmuyorsunuz.
Birkaç saniye sonra yüzünüze bir gülümseme geliyor. Başınızı kaldırıp doktora bakıyorsunuz.
“Test sonuçlarına bakarak, hasta olmam ihtimali ne kadardır sizce?”
“Ee, dedim ya, yüzde doksandokuz filan işte.”
“Hayır” diyorsunuz gülümseyerek. “Sadece yüzde bir!”
“Saçmalamayın!” Doktor kaşlarını çatıyor artık. Ama aldırmadan açıklıyorsunuz.
“Bakın, mesela bir milyon kişilik bir topluluk alalım ele. Hastalığın onbinde bir görüldüğünü söylediniz. O zaman bir milyon içinde yüz kişide bu hastalığı görmeyi bekleriz.”
Doktor donuk bir ifadeyle bakıyor, bitse de gitse gibisinden.
“Buna karşılık kalan 999 900 kişi hasta değil. Fakat yüzde bir ihtimalle, testin sağlıklı insanlarda pozitif sonuç verdiğini söylediniz. O zaman, hasta olmayanlar içinde 9999 kişide testin pozitif çıkmasını bekleriz.”
Doktorun kaşları hâlâ çatık, ama hafifçe başını sallıyor.
“Başka bir deyişle, bir milyon kişiye test yapsak, 10 099 kişi pozitif çıkar. Oysa gerçekten hasta olan sadece 100 kişi var. O zaman, testin pozitif çıkmasına bakarak hasta olmam ihtimali 100/10 099, yani yüzde bir bile değil!”
Hevesle elinizdeki kağıdı doktora uzatıyorsunuz. Şöyle bir bakıp bırakıyor.

“Olmaz öyle şey,” diyor doktor, “yanlışınız var.”
“Hesap açık doktor.”
“Hesapla olmaz bu işler efendim, tecrübe önemli. Biz bu kadar boşuna mı okuduk? Neyse, bekleyen hastalarım var, siz gidin biraz düşünün, sonra isterseniz tedaviye başlarız.”
Arkanızdan kapıyı çekerken “ukala dümbeleği” diye fısıldadığını duyuyorsunuz. Aldırmadan gülümsüyorsunuz. Başka bir uzman bulmanız gerekecek. Ama önce, parka gidip bu güzel günün tadını çıkaracaksınız.
Bu farazi diyalogda doktorun yaptığı hata epeyce yaygın bir yanılgıdır ve “temel oranı ihmal yanılgısı” olarak bilinir. İlk bakışta bir paradoks gibi görülüyor: Hasta olan herkesi tespit edebilen, hasta olmayanlarda ise sadece %1 yanılma payı olan bir test pozitif çıktığında, hasta olma ihtimali nasıl çok düşük çıkabilir?
Basitçe söylersek, temel oranın, yani rastgele seçilen bir insanın hasta olması ihtimalinin onbinde bir gibi çok küçük bir sayı olması sebebiyle. Yanlış alarm ihtimali sadece yüzde bir bile olsa, temel orandan çok daha yüksek. Bu yüzden de gerçek hastaların yüz katı kadar yanlış alarm gözlüyoruz. Bunu şematik olarak şöyle gösterebiliriz.
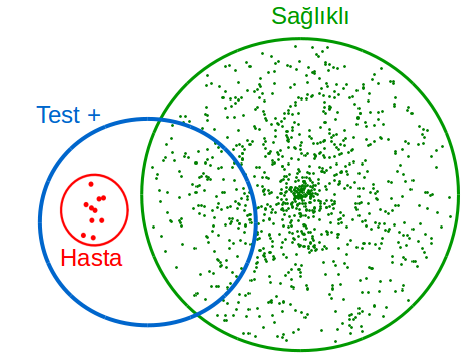
Yanılgının bize doğal gelmesinin sebeplerinden birisi de neden-sonuç ilişkisini tersine çeviriyor olmamız. Doktorun yüzde yüz dediği, hasta isek testin pozitif çıkması olasılığı. Ama bizim bilmemiz gereken, test pozitif çıktıysa hasta olma ihtimalimiz.
Daha gündelik bir örnek verelim: Bütün olimpik haltercilerin vücutları kaslıdır. “Kaslı olma”yı haltercilik testi diye düşünelim. Bir olimpik halterci için bu testin sonucu kesinlikle pozitiftir. Ama kaslı olan herkes olimpik halterci değildir. Rastgele seçilen kaslı birinin olimpik halterci olması ihtimali yine yüzde birden azdır.
Bunun için bir deyimimiz bile var: Her sakallıyı baban sanma! Temel oranı ihmal yanılgısı, özünde, her sakallıyı babamız sanmaktır.
O zaman doktorun yaptırdığı testin hiç faydası yok mu? Elbette var. Test yapmadan önce o hastalığa sahip olmamız olasılığı onbinde birdi, testten sonra yüzde bire yükseldi. Bu durumda iyi bir doktor size korkuya mahal olmadığını, ama daha kesin bilgi verecek muayeneler yapmak gerektiğini söyleyecektir.
Diyelim testimizin yanlış alarm oranı (sağlıklı olanlarda pozitif çıkma ihtimali) yüzde bir değil de, on binde bir olsun. Bu durumda bir milyon kişiden 100 kişi gerçekten hasta olacak, 100 sağlıklı kişide ise yanlış alarm verilecek. Böylece test sonucu pozitif ise hasta olma ihtimali 100/(100+100) = %50 olacak. Peki yanlış alarm oranı yüz binde bir ise? O da sizin ev ödeviniz.
Mizansenimizde doktora haksızlık yaptığımızı düşünebilirsiniz. Ancak temel oranı ihmal hatası, herkes gibi, doktorlar arasında da yaygın. Bunun en iyi bilinen örneklerinden biri, Harvard’da genç bir tıp öğrencisi olan Ward Casscells’in ve çalışma arkadaşlarının 1978’de yayınladığı araştırma.
Casscells, Harvard Tıp Okulu’nun koridorlarında dolaşıp, çevirdiği 60 hekim ve tıp öğrencisine şu soruyu sormuş: “Diyelim ki, toplumda yaygınlığı 1/1000 olan bir hastalığı tespit etmek için kullanılan bir test var ve bu testin hasta olmayanlarda pozitif çıkması ihtimali %5. Bu testi uyguladığımızda ve pozitif çıktığında, uygulanan kişinin hasta olması ihtimali nedir? Kişinin semptomları ve işaretleri hakkında hiç bir bilginiz olmadığını varsayın.”
Bu soruyu yukarıdaki yöntemle cevaplayabiliriz. Bin kişilik bir gruba test uyguladığımızı düşünelim. Bunların arasında bir kişi gerçekten hasta. Kalan 999 kişinin %5’inde, yani yaklaşık 50 kişide test yanlış alarm verecek. O zaman aranan ihtimal 1/51 olur, yani %2’den az.
Casscells ve arkadaşlarının görüştüğü altmış doktordan sadece onbiri cevabı doğru verebilmiş. Buna karşılık 27 doktor doğru olasılığın %95 olduğunu savunmuş, yani temel oranı ihmal yanılgısına düşmüş. Diğer cevaplar çok değişken; %0.095 de diyen var, %99 da. Cevapların ortalaması ise %56; gerçek olasılığın otuz katı.
Bunu basit ve önemsiz bir matematiksel oyun gibi görmek doğru olmaz. Temel oranı ihmal hatasının ciddi tıbbi sonuçları olabilir. Hasta olma ihtimalini olduğundan daha büyük zannederek riskli bir tedaviye başlanabilir ve hastanın hayatı gereksiz yere tehlikeye atılabilir. En azından, böyle bir teşhis hastada gereksiz bir endişe ve bunalım yaratır. O yüzden bir hekimin olasılıkları doğru tahmin edebilmesi ve aktarabilmesi şart.
İnsan zihni belirsizlikler karşısında bocalar. Bu bocalamanın üstesinden gelmek için bazı “kestirmeler” (heuristics) oluşturmuştur. Bu kestirme yollar, fazla düşünmeye gerek kalmadan hüküm vermemizi sağlar. Bu sayede tepki süremiz kısalır, önemli kararları kolayca verebiliriz.
Ancak bu kestirmeler bizi sık sık hataya da sürükler. 1970’lerden başlayarak davranışçı psikologlar, insanların hangi temel kestirmeleri kullandıklarını, bunların nasıl çalıştığını ve ne gibi düşünce hatalarına yol açtığını incelemeye başladılar. Temel oranı ihmal yanılgısı da bu bağlamda epeyce araştırıldı. Bu yanılgının, ve benzeri olasılık tahmini yanılgılarının (önceki bir yazımızda bahsettiklerimiz gibi), “temsiliyet kestirmesi” (representativeness heuristics) denen bir zihinsel şemadan kaynaklandığı düşünülüyor.
Temsiliyet kestirmesi, gördüğümüz bir numunenin, verilen bir açıklamaya uyma olasılığının tahmin edilmesidir. Şöyle açıklayalım: Diyelim Cüneyt 32 yaşında, atletik, motosiklete biniyor, güzel bir sarışınla çıkıyor. Şunlardan hangisi daha muhtemel? (a) Cüneyt bir öğretmen (b) Cüneyt bir futbolcu.
Çoğunluk, Cüneyt’in futbolcu olduğunu söyleyecektir. Ama şunu düşünün: Yüzbinlerce öğretmene karşılık sadece yüzlerce futbolcu var. Temel oranları ihmal yanılgısına düşüyoruz. Cüneyt’in öğretmen olma ihtimali, futbolcu olma ihtimalinin belki bin katı.
Neden bu yanılgıya düşüyoruz? Çünkü kafamızda öğretmenler ve futbolculara dair önyargılarla oluşturduğumuz bir kalıp var. Verilen tarif futbolcu kalıbını çok daha iyi temsil ediyor, tarifteki özelliklerin her iki meslekle de hiç bir ilgisi olmamasına rağmen. Öte yandan tarifi “saçı dökülmüş, evli, bilim kurgu okuru” şeklinde değiştirirsek muhtemelen cevapların çoğu değişecektir, çünkü bu yeni tarif kafamızdaki öğretmen kalıbını daha iyi temsil ediyor.
Hastalık testi örneğinde yapılan hata, Cüneyt örneğinde de geçerli. Cüneyt hakkında sorulan soru şu: “Bu tarife göre, Cüneyt’in futbolcu/öğretmen olması ihtimali nedir?”. Oysa zihnimizin duyduğu soru bunun tam tersi: “Cüneyt futbolcu/öğretmen ise, bu tarifin doğru olması olasılığı nedir?”
Temel oranı ihmal yanılgısının başka bir örneği olarak, yine psikoloji anketlerinde kullanılan bir soruyu, “taksi problemi”ni ele alalım.
Bir taksi gece vakti kaza yapıp kaçıyor. Şehirde iki taksi şirketi var: Yeşiller ve Maviler. Bütün taksilerin %85’i Yeşil, %15’i ise Mavi. Kazanın şahidi çarpan taksinin Mavi olduğunu söylüyor. Mahkeme, kazanın gerçekleştiği gecenin görüş şartlarında deney yaptırarak şahidin güvenilirliğini ölçtürüyor. Şahit her iki rengi %80 olasılıkla doğru teşhis ediyor, %20 olasılıkla yanılıyor.
Çarpan arabanın, şahidin ifadesine uygun olarak, gerçekten Mavi olması olasılığı nedir?
Yukarıda kullandığımız yöntemle bunu hesaplayabiliriz. Yüz taksiden onbeş tanesi Mavi’dir; şahit bunların onikisini (%80) doğru, üçünü (%20) ise yanlış teşhis edecek. Seksenbeş Yeşil taksiden altmışsekizini doğru teşhis ederken, onyedisinin yanlış olarak Mavi olduğunu iddia edecek, yani yanlış alarm verecek.

Şahit 100 taksiden 12+17, yani 29 aracın Mavi olduğunu iddia etti, ama sadece 12’si gerçekten Mavi. O zaman, şahit Mavi dediyse, aracın gerçekten Mavi olması ihtimali 12/(12+17) = %41’dir.
Şematik olarak gösterirsek

Ancak, pek çok kişi, şahidin haklı olması ihtimalini %80 civarı tahmin ediyor, yani taksilerin temel oranlarını ihmal ediyorlar. Nitekim, Yeşil ve Mavi taksiler eşit sayıda olsalardı bu cevap doğru olurdu (size ödev!), ama değiller.
Bu örnek, temel oranı ihmal yanılgısının nasıl hukuki sorunlar çıkarabileceğini gösteriyor. Gerçek bir adli vakada bir tahlil, test, veya şahit ifadesi delil olarak kritik rol oynuyorsa, avukat, savcı veya yargıcın temel oranı ihmal etmemeye, gerçek olasılıkları hesaplamaya zaman ayırmaları çok önemli. Aksi takdirde suçsuzlar haksız yere mahkum olabilirler.
Aynı yanılgı daha ciddi insan hakları ihallerine de yol açabilir. Şöyle bir senaryo düşünün: Hükümet terörle mücadele kapsamında çok gelişkin bir yüz tanıma sistemini devreye soktuğunu ilan ediyor. Sokaklarda, terminallerde, havaalanlarında, velhasıl bütün kamusal alanlardaki gözetleme kameraları sürekli olarak görüntü çekmekte, ve bu görüntüler bir merkezde analiz edilip arananların resimleriyle karşılaştırılmakta. Hükümet, bu sistemin %99 oranında isabetli oluşuyla övünüyor. Bütün kamuoyu bu atılımı alkışlıyor.
Ama siz, Yalansavar okuru olduğunuz için, yapılan ciddi hatayı hemen farkediyorsunuz. Temel oranı bilmeden, yüz tanıma sistemine bel bağlamak doğru değil. Biliyoruz ki teröristlerin temel oranı çok düşük. Diyelim, on bin kişiden sadece biri terörist (80 milyon içinde 8000 terörist – yüksek bir tahmin). Bu olasılıklar yazımızın başındaki hastalık teşhisi probleminin aynısı, o yüzden cevap elimizde hazır: Bu harika yüz tanıma sisteminin terörist diye işaretlediği birisinin gerçekten terörist olması ihtimali sadece %1.
Eğer yüz teşhisi sadece ilk aşamaysa, arkasından başka kontroller yapılacaksa bu o kadar da büyük bir sorun olmayacaktır. Ancak güvenlikle ilgili konularda toplumun akıldışılığa ve paranoyaya esir olması çok kolaydır. Hükümet, belki bilgisizlikten, belki kamuoyuna birşey yapıyor görüntüsü vermek için, veya belki baskı aracı olarak kullanma niyetiyle, bir teröristle beraber doksandokuz masumu tutuklamaktan çekinmeyebilir. Hatta, buradaki temel hataya işaret ederek uyarıda bulunanları ihanetle ve teröristlere yardım etmekle suçlayabilir.
Çok iyi bilinen bir gerçeği bu vesileyle tekrar hatırlıyoruz: Hukukun ve demokrasinin doğru işlemesi için toplumda esaslı bir temel eğitim ve bilimsel birikim olması şarttır. Aksi halde, siz bir yanlışı gösterdiğinizde, düzeltmeyi bırakın, neden bahsettiğinizi anlamazlar bile.
Meraklısına notlar
Bu yazıda teknik adıyla aslında Bayes teoreminden bahsediyorum. Bu teorem, şartlı olasılıklar verildiğinde, şartları ters çevirme formülünü verir. Yani mesela, hasta isek testin pozitif çıkma olasılığını ters çevirip, test pozitifse hasta olmamız olasılığını bulmak için Bayes formülünü kullanırız. Matematiksel ayrıntılara burada girmek istemedim, ilgilenenler daha matematiksel bir açıklamayı Wikipedia’dan okuyabilirler (İngilizce) veya Khan Academy’nin Türkçe açıklama videosunu seyredebilirler.
Dikkatli okurlar “hastalık ihtimali onbinde birdir” dedikten sonra, “onbin kişi alırsak bir tanesi hasta olacak” dememizi yadırgayabilirler, çünkü tabii ki bu ifade tam doğru değil. Rastgele seçilmiş onbin kişi arasında hiç hasta olmayabilir; iki hatta üç hasta da olabilir. Hasta sayısını bir rastgele değişken olarak düşündüğümüzde haklı bir itiraz, ama buradaki kastımız farklı. Olasılıkları reel sayılar yerine tam sayılarla ifade ettiğimizde bu problemleri anlamak ve çözmek nispeten daha kolay.
Temel oranı ihmal yanılgısının bilişsel kökenlerini inceleyen psikologlardan biri olan Gerd Gigerenzer’e göre, bu ve benzeri olasılık yanılgıları, insanların ondalıklı sayıları kullanmakta zorlanmalarından kaynaklanıyor. Bunun yerine problemi sayılamaya dayanan bir şekilde (“on bin kişiden biri hasta”) ifade etmek insan zihnine daha uygun oluyor ve doğru cevabı bulmak kolaylaşıyor. Bu sayılama yaklaşımında problemi öyle ifade ediyoruz ki, her alt grupta tamsayılar bulunmasını sağlıyoruz. Böylece ondalıklı sayıları çarpmanın bilişsel yükünden kurtuluyoruz, ve bizim için daha doğal olan bir yöntem kullanmış oluyoruz.
 Image copyrightDR LİSA RONAN
Image copyrightDR LİSA RONANBir araştırmaya göre aşırı kilolu insanların beyinleri, zayıf akranlarına göre 10 yıl daha yaşlı görünüyor.
İnsan beyni, bilgiyi ileten kısım olan ak maddeyi zamanla, yani yaşlandıkça doğal olarak kaybediyor.
Cambridge Üniversitesi’nde yapılan bir araştırma ise aşırı kilonun bu kaybı hızlandırdığını ortaya koydu.
Bir diğer deyişle 50 yaşındaki kilolu bir insan, 60 yaşındaki zayıf bir insanla aynı beyin yapısına sahip oluyor.
Cambridge Yaşlanma ve Nörobilim Merkezi’nde yapılan araştırmada 20-87 yaşlarındaki 473 kişi incelendi.
Kilonun beyindeki ak madde oranını ancak orta yaştan itibaren etkilediği görüldü.
Fakat bu farklılığın beynin işlevlerine nasıl yansıdığı henüz anlaşılamadı: Araştırmaya katılan kilolu ve zayıf gruplarda bilgi ve kavrayış açısından fark görülmedi.
Araştırmacılar şimdi kilonun örneğin demans gelişimini etkileyip etkilemediğini görmek için çalışmalarını sürdürmek istiyor.
Ekibin lideri Dr Lisa Ronan, kilonun mu beyni yoksa beynin mi kiloyu etkilediğini de henüz bilmediklerini söyledi.
Çalışmaya katılan bir diğer isim olan Profesör Sadal Farooqi ise kilo kaybı durumunda beyinde kaybolan ak maddenin yeniden oluşup oluşmadığını da ortaya çıkarmak istediklerini belirtiyor.
Yorum yazabilmek için oturum açmalısınız.